Chapter 6: Registration and Normalization
Overview
Although most people’s brains are similar - everyone has a cingulate gyrus and a corpus callosum, for instance - there are also differences in brain size and shape. As a consequence, if we want to do a group analysis we need to ensure that each voxel for each subject corresponds to the same part of the brain. If we are measuring a voxel in the visual cortex, for example, we would want to make sure that every subject’s visual cortex is in alignment with each other.
This is done by Registering and Normalizing the images. Just as you would fold clothes to fit them inside of a suitcase, each brain needs to be transformed to have the same size, shape, and dimensions. We do this by normalizing (or warping) to a template. A template is a brain that has standard dimensions and coordinates - standard, because most researchers have agreed to use them when reporting their results. That way, if you normalize your data to that template and find an effect at coordinates X=3, Y=20, Z=42, someone else who has warped their data to the same template can check their results against yours. The dimensions and coordinates of the template brain are also referred to as standardized space.
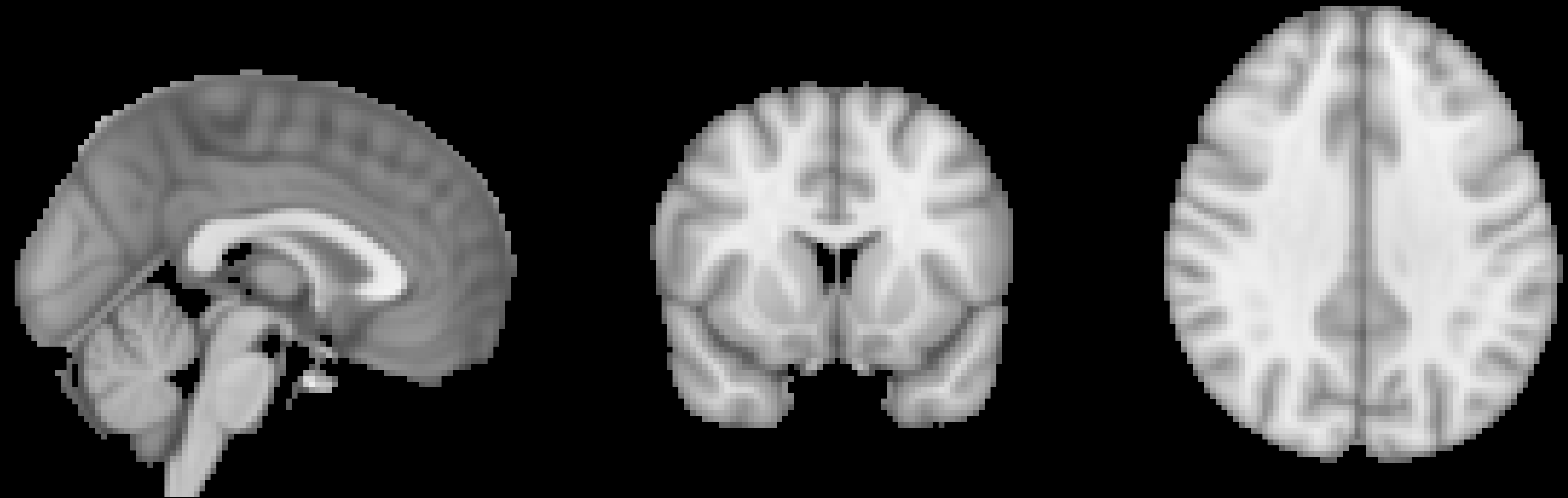
An example of a commonly used template, the MNI152 brain. This is an average of 152 healthy adult brains, which represent the population that most studies draw from. If you are studying another population - such as children or the elderly, for example - consider using a template created from representatives of that population. (Question: Why is this template blurry? Review the previous chapter on smoothing for a hint.)
Affine Transformations
To warp the images to a template, we will use an affine transformation. This is similar to the rigid-body transformation described above in Motion Correction, but it adds two more transformations: zooms and shears. Whereas translations and rotations are easy enough to do with an everyday object such as a pen, zooms and shears are more unusual - zooms either shrink or enlarge the image, while shears take the diagonally opposite corners of the image and stretch them away from each other. The animation below summarizes these four types of linear transformations.

Note
As with rigid-body transformations, zooms and shears each have three degrees of freedom: You can zoom or shear an image along the x-, y-, or z-axis. In total, then, affine transformations have twelve degrees of freedom. These are also called linear transformations because a transformation applied in one direction along an axis is accompanied by a transformation of equal magnitude in the opposite direction. A translation of one millimeter to the left, for example, implies that the image has been moved one millimeter from the right. Likewise, if an image is enlarged by one millimeter along the z-axis, it is enlarged by one millimeter in both directions along that axis. Transformations without these constraints are called nonlinear transformations. For example, a nonlinear transformation can enlarge the image in one direction while shrinking it in the other direction, as when squeezing a sponge. These types of transformations will be discussed later.
Registration and Normalization
Recall that we have both anatomical and functional images in our dataset. Our goal is to warp the functional images to the template so that we can do a group-level analysis across all of our subjects. Although it may seem reasonable to simply warp the functional images directly to the template, in practice that doesn’t work very well - the images are low-resolution, and therefore less likely to match up with the anatomical details of the template. The anatomical image is a better candidate.
Although this may not seem to help us towards our goal, in fact warping the anatomical image can assist with bringing the functional images into standardized space. Remember that the anatomical and functional scans are typically acquired in the same session, and that the subject’s head moves little, if at all, between the scans. If we have already normalized our anatomical image to a template and recorded what transformations were done, we can apply the same transformations to the functional images - provided they start in the same place as the anatomical image.
This alignment between the functional and anatomical images is called Registration. Most registration algorithms use the following steps:
Assume that the functional and anatomical images are in roughly the same location. If they are not, align the outlines of the images.
Take advantage of the fact that the anatomical and functional images have different contrast weightings - that is, areas where the image is dark on the anatomical image (such as cerebrospinal fluid) will appear bright on the functional image, and vice versa. This is called mutual information. The registration algorithm moves the images around to test different overlays of the anatomical and functional images, matching the bright voxels on one image with the dark voxels of another image, and the dark with the bright, until it finds a match that cannot be improved upon.
Once the best match has been found, then the same transformations that were used to warp the anatomical image to the template are applied to the functional images.

Normalization, Smoothing, and Statistical Power
As you read on the previous page, smoothing tends to cancel out noise and enhance signal. This applies to group analyses as well, in which all of the subjects’ images have been normalized to a template. Although each subjects’ functional images will be transformed to match the general shape and large anatomical features of the template, there will be variations in how smaller anatomical regions align among the normalized functional images. If the images are smoothed, there will be more overlap between clusters of signal, and therefore greater likelihood of detecting a significant effect.
The Registration Tab
Registration and Normalization, although distinct, are packaged together as a single step in the FEAT GUI’s Registration tab. Once you have selected this tab, click on the button next to Main structural image to expand the input field. Then select the subject’s skull-stripped image - in this case, the one that we created using a fractional intensity threshold of 0.2.
You will notice that there are dropdown menus below both the Main structural image and Standard space fields. The menus under the Main structural image field correspond to options for registering the functional to the anatomical image. The menus under the Standard space field are options for normalizing the anatomical image to the template image. Within these sets of menus, the dropdown menu on the left is the Search window, and the dropdown menu on the right is the Degrees of Freedom window.
In the Search window, there are three options: 1) No search; 2) Normal search; and 3) Full search. This signifies to FSL how much to search for a good initial alignment between the functional and anatomical images (for registration) and between the anatomical and template images (for normalization). The Full search option takes longer, but is more thorough and therefore more likely to produce better registration and normalization.
In the Degrees of Freedom window, you can use 3, 6, or 12 degrees of freedom to transform the images. Registration has an additional option, BBR, which stands for Brain-Boundary Registration. This is a more advanced registration technique that uses the tissue boundaries to fine-tune the alignment between the functional and anatomical images. Similar to the Full search option above, it takes longer, but often gives a better alignment.
For now, set both Search options to Full search and both Degrees of Freedom options to 12 DOF. If you have already loaded your functional images in the Data tab, click on the Go button to run all of the preprocessing steps.

Video
Registration and Normalization is the last step of the preprocessing pipeline for a single subject. To see a screencast video demonstrating how to set up all of your preprocessing through the FEAT GUI, click here.